Definição de critérios de projeto para circuitos de acionamento de bobinas e seleção de bobinas de relé
Introdução
As bobinas de relés e contactores são normalmente enroladas com fio de cobre - e o fio de cobre tem um coeficiente de temperatura positivo como se mostra nas fórmulas e no gráfico seguinte. A maioria das bobinas também são alimentadas por uma tensão relativamente fixa. Assim, supondo que a tensão permaneça constante, o aumento da temperatura resultará em maior resistência à bobina e diminuição da corrente da bobina.
A força do campo magnético nesses dispositivos depende diretamente das voltas por ampere (AT) (ou seja, o número de voltas do fio multiplicado pela corrente que flui através dele) dentro da bobina. Uma tensão fixa e um aumento da temperatura geram um menor número de AT e, assim, diminuem a força do campo magnético. Para que o relé ou contator opere e se mantenha de forma confiável ao longo do tempo, é preciso manter uma taxa de AT suficiente nas piores condições de temperatura, resistência da bobina, tolerância do enrolamento e tolerância à tensão de fornecimento. Caso contrário, o relé deixará de funcionar por completo, funcionará levemente com baixa força de contato ou cairá (liberação) inesperadamente. Todas essas condições são prejudiciais ao bom desempenho do relé.
Como o número de "voltas" do fio da bobina normalmente não é especificado nas folhas de dados, todas essas correções devem ser calculadas com base em temperaturas, resistências e tensões que são especificadas ou podem ser medidas.
A seguir há mais detalhes definindo critérios importantes de projeto para circuitos de acionamento de bobinas e seleção de bobinas de relé, um guia passo a passo para o processo e algumas fórmulas úteis. Consulte também a Nota de aplicação "O acionamento adequado da bobina é fundamental para o bom desempenho do relé e do contator”.
Análise
O acionamento adequado da bobina é extremamente importante para a operação correta do relé e um bom desempenho de carga/vida útil. Para que um relé (ou contator) funcione corretamente, é necessário garantir que a bobina seja adequadamente acionada para que os contatos se fechem corretamente e permaneçam fechados, e as bases da armadura fiquem totalmente assentadas e permaneçam assim em todas as condições possíveis durante a aplicação.
Os relés são eletroímãs, e a força do campo magnético que os opera é uma função da taxa das voltas por amperes (AT). Como o número de "voltas" não pode ser mudado, a única variável de aplicação é a corrente da bobina.
A corrente CC da bobina é determinada unicamente pela tensão aplicada e resistência da bobina. Se a tensão diminuir ou a resistência aumentar, a corrente da bobina diminuirá, resultando em um menor valor de AT e, portanto, redução da força magnética na bobina.
A corrente CA da bobina é igualmente afetada pela tensão aplicada e impedância da bobina, mas a impedância (Z) é definida como Z=sqrt(R2 + XL2 ), de modo que as alterações na resistência da bobina por si só têm um efeito um pouco menos direto nas bobinas CA do que nas bobinas CC.
A tensão aplicada da bobina também varia conforme a fonte de alimentação varia ao longo do tempo. O projetista do controle precisa definir a faixa de tensão de entrada sobre a qual o controle deve operar (tipicamente +10%/-20% do nominal) e, em seguida, compensar no projeto de controle para garantir o bom funcionamento nessa faixa de tensão.
Da mesma forma, a resistência da bobina apresentará uma tolerância de fábrica (tipicamente +/-5% ou +/-10%) a uma temperatura ambiente; mas a resistência do fio também tem um coeficiente de temperatura positivo, para que a resistência da bobina aumente ou diminua proporcionalmente às variações de temperatura do fio. Algumas fórmulas úteis:
Efeito da temperatura na resistência da bobina
Mudança da resistência da bobina em função da temperatura: Rf = Ri((Tf + 234,5) / (Ti + 234,5)) (Graficamente representada a seguir:)
Fator da resistência da bobina vs. temperatura da bobina
(Com base em 20 graus Celsius = 1 usando fio de cobre
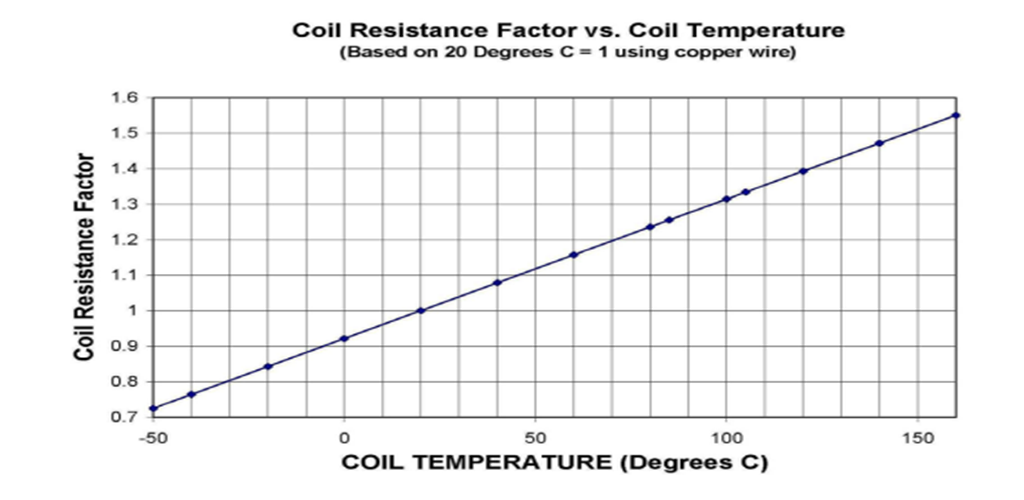
TEMPERATURA DA BOBINA (graus Celsius)
* Tensão de operação corrigida para a mudança de temperatura
Vf = Vo(Rf/Ri)
* Temperatura real da bobina pelo método "mudança de resistência"
Tf = Ti + Rf/Ri(k+Tri) – (k+Trt) [k = 234,5 para fio de cobre]
Usando as fórmulas acima e álgebra básica, é possível:
- Calcular a mudança da resistência esperada em função da temperatura
(certifique-se de incluir não apenas a temperatura ambiente, mas também o efeito do autoaquecimento do interior da bobina e do aquecimento causado pelos componentes internos de carga).
- Calcular a mudança esperada na tensão de operação
- Calcular o aumento da temperatura real da bobina e, assim, a resistência da bobina em diferentes condições (ou seja, temperatura ambiente sem alimentação, nenhuma carga à temperatura ambiente elevada com bobina alimentada e contatos totalmente carregados).
Definições de nomenclatura das fórmulas acima:
- Ri = Resistência da bobina na temperatura inicial da bobina
- Rf = Resistência da bobina na temperatura final da bobina
- Ti = Temperatura inicial da bobina
- Tf = Temperatura final da bobina
- Tri =Temperatura ambiente no início do teste
- Trt =Temperatura ambiente no final do teste
- Vo = Tensão de operação original
- Vf = Tensão de operação final (corrigida para a mudança de temperatura da bobina).
A temperatura "ambiente" é aquela nas proximidades do relé, não aquela nas proximidades do conjunto ou do invólucro que abriga o relé.
Da mesma forma, a "temperatura inicial da bobina" e "temperatura ambiente inicial" podem não ser exatamente as mesmas no início do teste, a menos que tempo suficiente tenha passado para que ambas se estabilizem.
Como as bobinas e outros componentes têm massa térmica, é preciso haver tempo suficiente para que todas as temperaturas se estabilizem antes de as medições serem registradas.
Correção da tensão da bobina CC para o cenário das piores condições
(Nota: pressupõe-se sempre que relés de bobina CC estejam sendo alimentados por CC bem filtrada, não por meia onda não filtrada ou por ondas completas, a menos que isso seja especificamente observado. Pressupõe-se, também, que as informações da ficha técnica, como as da resistência da bobina, tenham sido especificadas à temperatura ambiente (aproximadamente. 23 °C, a menos que seja observado em contrário).
As piores condições de operação de um relé são especificadas a tensão mínima de alimentação e resistência máxima da bobina à temperatura ambiente mais alta, sob o maior nível de carga de corrente no contato.
Desse modo, o projetista precisa corrigir a tensão de entrada nas bobinas dos relés para se adequar ao aumento da resistência da bobina e diminuição de AT, de modo que, no pior cenário, ainda haja AT suficiente para operar o relé e assentar completamente a armadura. Isso garantirá que a inteira força seja aplicada nos contatos. Se o contato for fechado, mas a armadura não estiver totalmente assentada, a força de contato será baixa e, portanto, os contatos ficarão sujeitos ao superaquecimento e propensos à soldagem de aderência após a aplicação de altas correntes.
Como é difícil calcular o aquecimento interno da bobina e da carga nos contatos, a maneira mais precisa de iniciar esse cálculo é pegar um relé de amostra do mesmo tipo e com a mesma tensão nominal da bobina e seguir estas etapas:
- Meça a resistência "Ri" da bobina à temperatura ambiente e registre os parâmetros de temperatura ambiente "Ti" e "Tri" para uso posterior.
- Carregue o contato na corrente máxima e aplique a tensão nominal na bobina.
- Aguarde a estabilização da temperatura da bobina (ou seja, até a resistência da bobina parar de variar), então meça a resistência "Rf" da bobina "quente". Isso dirá qual foi o "aumento de temperatura" na bobina causado pela corrente nos contatos e na bobina. Também meça qualquer alteração na temperatura ambiente e registre isso como o valor "Trt", para uso posterior.
- Em seguida, adicione a diferença entre a temperatura ambiente e a temperatura ambiente máxima esperada à resistência da bobina carregada acima. Usando a fórmula "Rf" ou o gráfico, corrija a resistência da bobina "quente" medida acima para o aumento da temperatura ambiente. Esse valor passará a ser o "Rf" corrigido.
- Utilizando a fórmula anterior "Vf = Vo(Rf/Ri)", calcule o novo valor para "Vf", utilizando a tensão de operação mínima fornecida na ficha técnica. (ou seja, a tensão nominal da bobina menos a tolerância negativa na tensão mínima de operação fornecida na folha de dados (geralmente 80% da nominal) para bobinas CC).
- O resultado disso será a tensão mínima que precisa ser aplicada na bobina do relé para que o funcionamento seja adequado sob as piores condições de operação.
Correção da bobina CA
- Nota: embora a correção das bobinas CA seja feita da mesma forma, é bom lembrar que a mudança de resistência (R) afeta a impedância das bobinas CA, como representado pela fórmula Z=sqrt(R2 + XL 2), em vez de afetá-las linearmente, de modo que o efeito na corrente da bobina, e consequentemente em AT, é também não linear. Consulte o parágrafo intitulado "Características de relés de bobina CA e contatores" da Nota de aplicação da TE "O acionamento adequado da bobina é fundamental para o bom desempenho do relé e do contator".
Conclusão
Consulte a Engenharia de Produto da TE para obter assistência caso uma combinação aceitável da faixa de tensão aplicada e valores disponíveis de uma bobina não seja compatível com a faixa de temperatura ambiente necessária na sua aplicação.
Isenção de responsabilidade
A TE fez todos os esforços razoáveis para confirmar a exatidão das informações aqui apresentadas; no entanto, a TE não garante que esteja livre de erros, nem faz qualquer outra representação, garantia ou endossa que as informações são precisas, corretas, confiáveis ou atuais. A TE SE ISENTA EXPRESSAMENTE DE TODAS AS GARANTIAS RELATIVAS ÀS INFORMAÇÕES AQUI CONTIDAS, SEJAM EXPRESSAS, IMPLÍCITAS OU ESTATUTÁRIAS, INCLUINDO QUAISQUER GARANTIAS IMPLÍCITAS OU COMERCIALIZAÇÃO OU ADEQUAÇÃO PARA UM PROPÓSITO ESPECÍFICO. Em nenhum caso a TE será responsável por quaisquer danos diretos, indiretos, incidentais, especiais ou consequentes decorrentes ou relacionados ao uso das informações pelo Destinatário.
Definição de critérios de projeto para circuitos de acionamento de bobinas e seleção de bobinas de relé
Introdução
As bobinas de relés e contactores são normalmente enroladas com fio de cobre - e o fio de cobre tem um coeficiente de temperatura positivo como se mostra nas fórmulas e no gráfico seguinte. A maioria das bobinas também são alimentadas por uma tensão relativamente fixa. Assim, supondo que a tensão permaneça constante, o aumento da temperatura resultará em maior resistência à bobina e diminuição da corrente da bobina.
A força do campo magnético nesses dispositivos depende diretamente das voltas por ampere (AT) (ou seja, o número de voltas do fio multiplicado pela corrente que flui através dele) dentro da bobina. Uma tensão fixa e um aumento da temperatura geram um menor número de AT e, assim, diminuem a força do campo magnético. Para que o relé ou contator opere e se mantenha de forma confiável ao longo do tempo, é preciso manter uma taxa de AT suficiente nas piores condições de temperatura, resistência da bobina, tolerância do enrolamento e tolerância à tensão de fornecimento. Caso contrário, o relé deixará de funcionar por completo, funcionará levemente com baixa força de contato ou cairá (liberação) inesperadamente. Todas essas condições são prejudiciais ao bom desempenho do relé.
Como o número de "voltas" do fio da bobina normalmente não é especificado nas folhas de dados, todas essas correções devem ser calculadas com base em temperaturas, resistências e tensões que são especificadas ou podem ser medidas.
A seguir há mais detalhes definindo critérios importantes de projeto para circuitos de acionamento de bobinas e seleção de bobinas de relé, um guia passo a passo para o processo e algumas fórmulas úteis. Consulte também a Nota de aplicação "O acionamento adequado da bobina é fundamental para o bom desempenho do relé e do contator”.
Análise
O acionamento adequado da bobina é extremamente importante para a operação correta do relé e um bom desempenho de carga/vida útil. Para que um relé (ou contator) funcione corretamente, é necessário garantir que a bobina seja adequadamente acionada para que os contatos se fechem corretamente e permaneçam fechados, e as bases da armadura fiquem totalmente assentadas e permaneçam assim em todas as condições possíveis durante a aplicação.
Os relés são eletroímãs, e a força do campo magnético que os opera é uma função da taxa das voltas por amperes (AT). Como o número de "voltas" não pode ser mudado, a única variável de aplicação é a corrente da bobina.
A corrente CC da bobina é determinada unicamente pela tensão aplicada e resistência da bobina. Se a tensão diminuir ou a resistência aumentar, a corrente da bobina diminuirá, resultando em um menor valor de AT e, portanto, redução da força magnética na bobina.
A corrente CA da bobina é igualmente afetada pela tensão aplicada e impedância da bobina, mas a impedância (Z) é definida como Z=sqrt(R2 + XL2 ), de modo que as alterações na resistência da bobina por si só têm um efeito um pouco menos direto nas bobinas CA do que nas bobinas CC.
A tensão aplicada da bobina também varia conforme a fonte de alimentação varia ao longo do tempo. O projetista do controle precisa definir a faixa de tensão de entrada sobre a qual o controle deve operar (tipicamente +10%/-20% do nominal) e, em seguida, compensar no projeto de controle para garantir o bom funcionamento nessa faixa de tensão.
Da mesma forma, a resistência da bobina apresentará uma tolerância de fábrica (tipicamente +/-5% ou +/-10%) a uma temperatura ambiente; mas a resistência do fio também tem um coeficiente de temperatura positivo, para que a resistência da bobina aumente ou diminua proporcionalmente às variações de temperatura do fio. Algumas fórmulas úteis:
Efeito da temperatura na resistência da bobina
Mudança da resistência da bobina em função da temperatura: Rf = Ri((Tf + 234,5) / (Ti + 234,5)) (Graficamente representada a seguir:)
Fator da resistência da bobina vs. temperatura da bobina
(Com base em 20 graus Celsius = 1 usando fio de cobre

TEMPERATURA DA BOBINA (graus Celsius)
* Tensão de operação corrigida para a mudança de temperatura
Vf = Vo(Rf/Ri)
* Temperatura real da bobina pelo método "mudança de resistência"
Tf = Ti + Rf/Ri(k+Tri) – (k+Trt) [k = 234,5 para fio de cobre]
Usando as fórmulas acima e álgebra básica, é possível:
- Calcular a mudança da resistência esperada em função da temperatura
(certifique-se de incluir não apenas a temperatura ambiente, mas também o efeito do autoaquecimento do interior da bobina e do aquecimento causado pelos componentes internos de carga).
- Calcular a mudança esperada na tensão de operação
- Calcular o aumento da temperatura real da bobina e, assim, a resistência da bobina em diferentes condições (ou seja, temperatura ambiente sem alimentação, nenhuma carga à temperatura ambiente elevada com bobina alimentada e contatos totalmente carregados).
Definições de nomenclatura das fórmulas acima:
- Ri = Resistência da bobina na temperatura inicial da bobina
- Rf = Resistência da bobina na temperatura final da bobina
- Ti = Temperatura inicial da bobina
- Tf = Temperatura final da bobina
- Tri =Temperatura ambiente no início do teste
- Trt =Temperatura ambiente no final do teste
- Vo = Tensão de operação original
- Vf = Tensão de operação final (corrigida para a mudança de temperatura da bobina).
A temperatura "ambiente" é aquela nas proximidades do relé, não aquela nas proximidades do conjunto ou do invólucro que abriga o relé.
Da mesma forma, a "temperatura inicial da bobina" e "temperatura ambiente inicial" podem não ser exatamente as mesmas no início do teste, a menos que tempo suficiente tenha passado para que ambas se estabilizem.
Como as bobinas e outros componentes têm massa térmica, é preciso haver tempo suficiente para que todas as temperaturas se estabilizem antes de as medições serem registradas.
Correção da tensão da bobina CC para o cenário das piores condições
(Nota: pressupõe-se sempre que relés de bobina CC estejam sendo alimentados por CC bem filtrada, não por meia onda não filtrada ou por ondas completas, a menos que isso seja especificamente observado. Pressupõe-se, também, que as informações da ficha técnica, como as da resistência da bobina, tenham sido especificadas à temperatura ambiente (aproximadamente. 23 °C, a menos que seja observado em contrário).
As piores condições de operação de um relé são especificadas a tensão mínima de alimentação e resistência máxima da bobina à temperatura ambiente mais alta, sob o maior nível de carga de corrente no contato.
Desse modo, o projetista precisa corrigir a tensão de entrada nas bobinas dos relés para se adequar ao aumento da resistência da bobina e diminuição de AT, de modo que, no pior cenário, ainda haja AT suficiente para operar o relé e assentar completamente a armadura. Isso garantirá que a inteira força seja aplicada nos contatos. Se o contato for fechado, mas a armadura não estiver totalmente assentada, a força de contato será baixa e, portanto, os contatos ficarão sujeitos ao superaquecimento e propensos à soldagem de aderência após a aplicação de altas correntes.
Como é difícil calcular o aquecimento interno da bobina e da carga nos contatos, a maneira mais precisa de iniciar esse cálculo é pegar um relé de amostra do mesmo tipo e com a mesma tensão nominal da bobina e seguir estas etapas:
- Meça a resistência "Ri" da bobina à temperatura ambiente e registre os parâmetros de temperatura ambiente "Ti" e "Tri" para uso posterior.
- Carregue o contato na corrente máxima e aplique a tensão nominal na bobina.
- Aguarde a estabilização da temperatura da bobina (ou seja, até a resistência da bobina parar de variar), então meça a resistência "Rf" da bobina "quente". Isso dirá qual foi o "aumento de temperatura" na bobina causado pela corrente nos contatos e na bobina. Também meça qualquer alteração na temperatura ambiente e registre isso como o valor "Trt", para uso posterior.
- Em seguida, adicione a diferença entre a temperatura ambiente e a temperatura ambiente máxima esperada à resistência da bobina carregada acima. Usando a fórmula "Rf" ou o gráfico, corrija a resistência da bobina "quente" medida acima para o aumento da temperatura ambiente. Esse valor passará a ser o "Rf" corrigido.
- Utilizando a fórmula anterior "Vf = Vo(Rf/Ri)", calcule o novo valor para "Vf", utilizando a tensão de operação mínima fornecida na ficha técnica. (ou seja, a tensão nominal da bobina menos a tolerância negativa na tensão mínima de operação fornecida na folha de dados (geralmente 80% da nominal) para bobinas CC).
- O resultado disso será a tensão mínima que precisa ser aplicada na bobina do relé para que o funcionamento seja adequado sob as piores condições de operação.
Correção da bobina CA
- Nota: embora a correção das bobinas CA seja feita da mesma forma, é bom lembrar que a mudança de resistência (R) afeta a impedância das bobinas CA, como representado pela fórmula Z=sqrt(R2 + XL 2), em vez de afetá-las linearmente, de modo que o efeito na corrente da bobina, e consequentemente em AT, é também não linear. Consulte o parágrafo intitulado "Características de relés de bobina CA e contatores" da Nota de aplicação da TE "O acionamento adequado da bobina é fundamental para o bom desempenho do relé e do contator".
Conclusão
Consulte a Engenharia de Produto da TE para obter assistência caso uma combinação aceitável da faixa de tensão aplicada e valores disponíveis de uma bobina não seja compatível com a faixa de temperatura ambiente necessária na sua aplicação.
Isenção de responsabilidade
A TE fez todos os esforços razoáveis para confirmar a exatidão das informações aqui apresentadas; no entanto, a TE não garante que esteja livre de erros, nem faz qualquer outra representação, garantia ou endossa que as informações são precisas, corretas, confiáveis ou atuais. A TE SE ISENTA EXPRESSAMENTE DE TODAS AS GARANTIAS RELATIVAS ÀS INFORMAÇÕES AQUI CONTIDAS, SEJAM EXPRESSAS, IMPLÍCITAS OU ESTATUTÁRIAS, INCLUINDO QUAISQUER GARANTIAS IMPLÍCITAS OU COMERCIALIZAÇÃO OU ADEQUAÇÃO PARA UM PROPÓSITO ESPECÍFICO. Em nenhum caso a TE será responsável por quaisquer danos diretos, indiretos, incidentais, especiais ou consequentes decorrentes ou relacionados ao uso das informações pelo Destinatário.
